Lab Math, Medical Math & Data Analysis

Monika Oli

Modules – Skills & Tools

Lab Math, Medical Math & Data Analysis

Background Information

WHY YOU SHOULD CARE ABOUT… Lab & Medical Math

Basic math skills are essential in every day life, from cooking to calculating discounts at the store. For scientists and health care workers and clinical staff, basic math concepts translate to life and death of their patients. I promise that the math we do in this module and throughout the class is no more complicated than 5th or 6th grade math – and I am very confident that you all will excel. Many student have math anxiety, because they tell themselves they are not good at math or a teacher once said that. Ignore that and come with a fresh mind to think how exciting it is to apply useful and applied basic math in the lab and for your future careers.

Einstein

WHY YOU SHOULD CARE ABOUT… Data Analysis

There is no point in doing experiments and collecting data if you don’t know how to critically evaluate and analyze your data. The first step is always to look at raw data, check if there are outliers, did the data get entered correctly into the spreadsheet, do the results look good and follow the experimental design you implemented? After basic graphing of data you can continue with descriptive statistics, and visualization of your results. Checking for normal distribution of your data is important for many statistical tests that follow. Genomic data analysis has become a lot more challenging as “big data” are hard to visualize in a simple graph. Careful curation of data and knowledge of advance analysis through command line based programs is important. Advanced analysis could include modeling of data for future prediction of outcomes.

Learning Objectives

After completing this module, students will be able to:

Recall new vocabulary and definitions that pertain to this module.
Calculate ratios, fractions, percentages and calculate v//v or w/v.
Create molar solutions and dilutions.
Calculate various dilutions using c1v1 = c2v2.
Determine CFU/ml from a variety of serial dilution experiments.
Use scientific notation and it’s conventions and conversions throughout the class and your ELN
Appreciate basic math concepts in every day life and for your future careers
Understand design of experiments including replica and controls
Visualize and evaluate sets of data
Conduct basic descriptive statistics and use functions in Excel
Produce graphs from data, including error bars or box plots and proper labels on all elements (according to instructions to authors)
Interpret results and compose figure legends

Metric and English Measurement Equivalents

The Metric System

The metric system comprises three basic units of measurement: distance measured in meters, volume measured in liters, and mass measured in grams. In order to designate larger and smaller measures, a system of prefixes based on multiples of ten is used in conjunction with the basic unit of measurement. The most common prefixes are:

kilo = 103 = 1,000

centi = 10-2 = 0.01

milli = 10-3 = 0.001

micro = 10-6 = 0.000001

nano = 10-9 = 0.000000001

Scientific Notation

Microbiologists often have to deal with either very large or very small numbers, such as 5,550,000,000 or 0.00000082. The mere manipulation of these numbers is cumbersome. As a result, it is more convenient to express such numbers in scientific notation (standard exponential notation). Scientific notation is a set of rules involving a shorthand method for writing these numbers and performing simple manipulations with them. Scientific notation uses the fact that every number can be expressed as the product of two numbers – one of which is a power of the number 10. Numbers greater than 1 can be expressed as follows:

In the above notations, the exponent to which the l0 is raised is equal to the number of zeros following the 1. Numbers less than 1 can be expressed as follows:

History Connection

Case Study

Sebastian Ferrero died at Shands Hospital in Gainesville, Florida in October 2007, at age 3, as a result of a medication overdose followed by a series of preventable medical errors. Check out his story:

Next time you are at Shands, visit the Sebastian Ferrero Atrium at the bottom of the pediatrics unit.

Online and In-Person Labs

Activity: Learn how to solve common lab math problems.

These are the calculations you will learn:

Making stock solutions
Making molar concentrations (w/v) and concentrations weight/volume (w/v %)
To dilute a solution to an unspecified final volume in just one step
To dilute a solution to a specified final volume in just one step
To dilute a solution to an unspecified final volume in several steps
To dilute a solution to a specified final volume in several steps
Serial dilutions

Lab Kit Materials for this Activity:

Computer/ Laptop

Video Tutorials

Lab Math Sample Problem Work-Through

Procedures

A. Molar Concentrations

1) How you would make 500mL of a 0.05M NaCl solution.
2) How much arginine do you need to make a 0.01M solution of arg (MW = 174.20)?
3) How much arginine do you need to make 100 ml of a 0.01M solution of arg (MW = 174.20)?

B. Concentrations weight/volume (w/v)

1) How much NaCl do you need to weigh out to make 1L of a 0.9 % NaCl solution?

C. Diluting a Solution to an Unspecified Volume in Just One Step

1) If you have a 1M arg stock and you want on inject a 100 ml of a 1mM solution– What do you use to dilute the stock?
2) Dilute a solution that has an initial concentration of solute of 10% down to 2%.
3) Dilute a solution that has an initial concentration of 0.01% to 0.0001%.

D. Diluting a Solution to a Specified Volume in Just One Step

1) You have a 0.01% solution. You want a 0.001% solution and you need 25 ml.
2) Prepare 50 ml of a 3% solution from a 4% solution.
3) Prepare 100 ml of 10% alcohol from 95% alcohol.
4) You need 45 ml of 50% alcohol. How can you prepare this from 70% alcohol?
5) What volume of a 20% dextrose broth solution should be used to prepare 250 ml of 1% dextrose broth?
6) Prepare a 45 ml of a 2% suspension of Red Blood Cells (RBCs) from a 5% suspension.
7) What volume of a 0.02% solution can be prepared from 25 ml of a 0.1 % solution?
8) What percent concentration of alcohol is prepared when 10 ml of 95% alcohol are diluted with H20 to make a final volume of 38 ml?
9) What percent of dextrose is prepared when 3 ml of a 10% dextrose solution are mixed with 12 ml of broth?

E. Diluting a Solution to an Unspecified Volume in Several Steps

1) You have a stock solution of protein containing 10 grams per ml. You want a concentration of 2 mg/ml. How would you perform this dilution in just three steps?
2) You have a stock solution of 10 mg/ml of vitamins and want to obtain a solution of 0.5 μg/ml. How would you perform this dilution in just three steps?

F. Diluting a Solution to a Specified Volume in Several Steps

1) You want a 1:128 dilution of serum and you need 4 ml. How would you perform this dilution in several steps?
2) You want a 1:3,000 dilution of serum and you need 2 ml. How would you perform this dilution in several steps?
3) How would you prepare 1 ml of a 1:5 dilution of sera?
4) How would you prepare 8 m1 of a 1:20 dilution of sera?

G. Serial dilutions

1) Based on the following dilutions, how many bacteria were present in the original sample?

Dilution problem

2) How many bacteria were present in the original sample (CFU/ml)?

Dilution	Volume Plated	Colonies Counted
10-3	1.0 ml	TNTC
10-4	1.0 ml	256
10-5	1.0 ml	21
10-6	1.0 ml	7
10-7	1.0 ml	0
10-8	1.0 ml	1

3) If 0.1 ml of a urine culture from a 10-6 dilution yielded 38 colonies, how many bacteria were there per ml in the original sample?

4) How many bacteria were present in the following sample?

Dilution	Volume Plated	Number of Colonies Counted
10-7	0.1 ml	26

5) How many bacteria were present in the following sample?

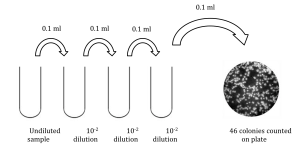
6) How many bacteria were present in the original sample?

SOLUTIONS:

Question	Work	Solution
A1	MW NaCl = 58.44 58.44 g ~ 1M ~ 1L 29.22 g ~ 1M ~ 0.5L Dilution factor: 1M/0.05M = 20 (fold dilution) ~ 29.22/20 = 1.461 1.461 g ~ 0.05M ~ 0.5L	You weigh out 1.46g and fill to 500 ml
A2	MW arg = 174.20 174.20 ~ 1M ~ 1L Dilution factor: 1M/0.01M = 100 fold 1.742 g ~ 0.01M ~ 1L	You weigh out 1.74g and fill to 1000 ml
A3	MW arg = 174.20 174.20 ~ 1M ~ 1L Dilution factor: 1M/0.01M = 100 fold 1.742 g ~ 0.01M ~ 1L 0.74 g ~ 0.01M ~ 0.1L	You weigh out 0.174g and fill to 100 ml
B1		9 g NaCl – fill to 1L with water
C1	C1 x v1 = c2 x v2 1M x ? ml = 0.001M x 100 ml ? = (0.001 M x 100 ml)/1M = 0.1 ml	Add 0.1 ml of the stock solution to 99.9 ml STERILE saline solution
C2	Take 1 volume of the initial concentration (10%) and 4 volumes of solvent for a total of 5 volumes: 1 ml of a 10% solution + 4 ml of diluent will give a total of 5 ml and each ml will now contain 2% instead of 10%
C3	In order to obtain a 0.0001% solution from a 0.01% solution, the latter must be diluted 100 times. Take 1 volume of the initial concentration (0.01%) and add 99 volumes of solvent for a total of 100 volumes. 1 ml of 0.01% solution + 99 ml of diluent will give a total of 100 ml and each ml now contains 0.0001% instead of 0.01%.
D1	A 0.01% solution is 10 times more concentrated than the 0.001% solution. Divide the number of times the 10 must be diluted into the final volume specified: 25/10 = 2.5. 2.5 ml of a 0.01% solution + 22.5 ml of diluent will give a total of 25 ml and each ml now contains 0.001%.

D2	C1 = 4%, C2 = 3%, V2 = 50 ml, V1 = X (0.04)X = (0.03)(50) X = 37.5 ml	Thus, 37.5 ml of a 4% solution + 12.5 ml of solvent = 50 ml of 3% solution.
D3	C1 = 95%, C2 = 10%, V2 = 100 ml, V1 = X (0.95)X = (0.10)(100) X = 10.5 ml	Thus, 10.5 ml of a 95% alcohol + 89.5 ml of H2O = 100 ml of a 10% alcohol solution.
D4	C1 = 70%, C2 = 50%, V2 = 45 ml, V1 = X (0.7)X = (0.5)(45) X = 32.1	Thus, 32.1 ml of 70% alcohol +12.9 of H2O = 45 ml of a 50% alcohol solution.
D5	C1 = 20%, C2 = 1%, V2 = 250 ml, V1 = X (0.2)X = (0.01)(250) X = 12.5 ml	Thus, 12.5 ml of a 20% solution + 237.5 of broth = 250 ml of a 1% dextrose broth solution.
D6	C1 = 5%, C2 = 2%, V2 = 45 ml, V1 = X (0.05)X = (0.02)(45) X = 18 ml	Thus, 18 ml of 5% + 27 ml of saline = 45 ml of 2% red blood cell suspension.
D7	C1 = 0.1%, C2 = 0.02%, V2 = X, V1 = 25 ml (0.001)(25)= (0.0002)X X = 125 ml	Thus, prepare a total volume of 125 of a 0.02% solution from 25 ml of 0.01% solution by adding 100 ml of diluent to the latter.
D8	C1 = 95%, C2 = X, V2 = 38 ml, V1 = 10 ml (0.95)(10) = X(38) X = 25%
D9	C1 = 10%, C2 = X, V2 = 15 ml, V1 = 3 ml (0.10)(3) = X(15) X = 2%
E1	In order to make all units equal, you have to convert 10 grams into milligrams. Stock solution = 10,000 mg/ml. Final concentration = 2 mg/ml IC/FC = 10,000 / 2 = 5,000 Thus the Dilution Factor is 5,000. To perform a 1: 5,000 dilution, 1 ml of 10,000 mg/ml stock solution + 49 ml of diluent = 1:50 dilution = 200 mg/ml 1 ml of 200 mg/ml + 9 ml of diluent = 1:10 dilution = 20 mg/ml 1 ml of 20 mg/ml + 9 ml of diluent = 1:10 dilution = 2 mg/ml
E2	Make all the units the same. Convert 10 mg into micrograms. Stock solution = 10,000 ug/ml. Final concentration = 0.5 ug/ml. IF/FC = 10,000 / 0.5 = 20,000 Thus, the Dilution Factor is 20,000. To perform a 1:20,000 dilution 1 ml of 10,000 mg/ml +19 ml of diluent = 1:20 dilution = 500 mg/ml 1 ml of 500 mg/ml + 99 ml of diluent = 1:100 dilution = 5 mg/ml 1 ml of 5 mg/ml + 9 ml of diluent = 1:10 dilution = 0.5 mg/ml
G1	The first step is to establish the initial dilution as follows: 128/4 = 32 1:32 is the first step dilution, and the second is 1:4. Step 1 – 1 ml of serum + 31 ml of diluent = 1:32 (individual dilution) Step 2 – 1 ml of 1:32 dilution + 3 ml of diluent = 1:4 (individual dilution)
G2	We can obtain a 1:3,000 dilution in three steps by using 1:30 and 1:10 dilutions. 3000 / 2 = 1,500 Step 1 – 1 ml of serum + 29 ml of diluent = 1:30 (individual dilution) Step 2 – 1 ml of 1:30 dilution + 9 ml = 1:10 (individual dilution) Step 3 – 1 ml of 1:10 dilution + 9 ml = 1:10 (individual dilution)
G3	D1 = 1, D2 = 5, V1 = X, V2 = 1 D1/D2 = V1/V2 1 / 5 = X / 1 X = 0.2 ml	Thus, 0.2 ml (undiluted serum) + 0.8 ml of saline = 1.0
G4	D1 = 1, D2 = 20, V1 = X, V2 = 8 D1/D2 = V1/V2 1 / 20 = X / 8 X = 0.4 ml	Thus, 0.4 ml (undiluted serum) + 7.6 ml of saline = 1:20
G5		2.01 x 106 CFU/ml
G6		2.56 x 106 CFU/ml

Results

Document the following in your ELN:

Why is it important to be able to perform accurate calculations in the laboratory and medical fields? What can result from improper calculations (refer to case study)?
Know how to convert between units and scientific notation.
Complete practice problems from each section above. There will be lab math questions on your midterm- be prepared by practicing until you are comfortable.

Resources

LabMath Apps

After you have gone through the module and really understand all the calculations, you can use a labmath calculator to double check your calculations or if you do frequent calculations in the lab. The best ones I have used are:

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License